Some time ago, I set out on a journey to understand "What kinds of problems can quantum computation solve efficiently?" I decided to write a series of blog posts to explain this as simply as possible. In previous posts, I discussed the qubit and measurement. In this post, I will finally answer the question. The most common answer is, "It can run computations in parallel." However, as I showed in the previous post about measurement, that is not exactly true. A quantum computer cannot simulate a computer with the enormous number of processors. However, it can simulate a different kind of machine in some special cases: the Nondeterministic Turing machine.
Nondeterministic Computing machine
I will not go into the details of Turing machines, but I need to describe nondeterminism in computing machines. A nondeterministic computing machine (my own term to avoid details of the Turing machine) is a theoretical or hypothetical machine. One perspective is that the machine can solve problems for which it is easy to verify a solution, but hard to find one. For example, it is easy to verify that an integer \(a\) divided by integer \(b\) has remainder 0, but it is hard to find such number \(b\). By "hard," I mean it takes a lot of computation steps.
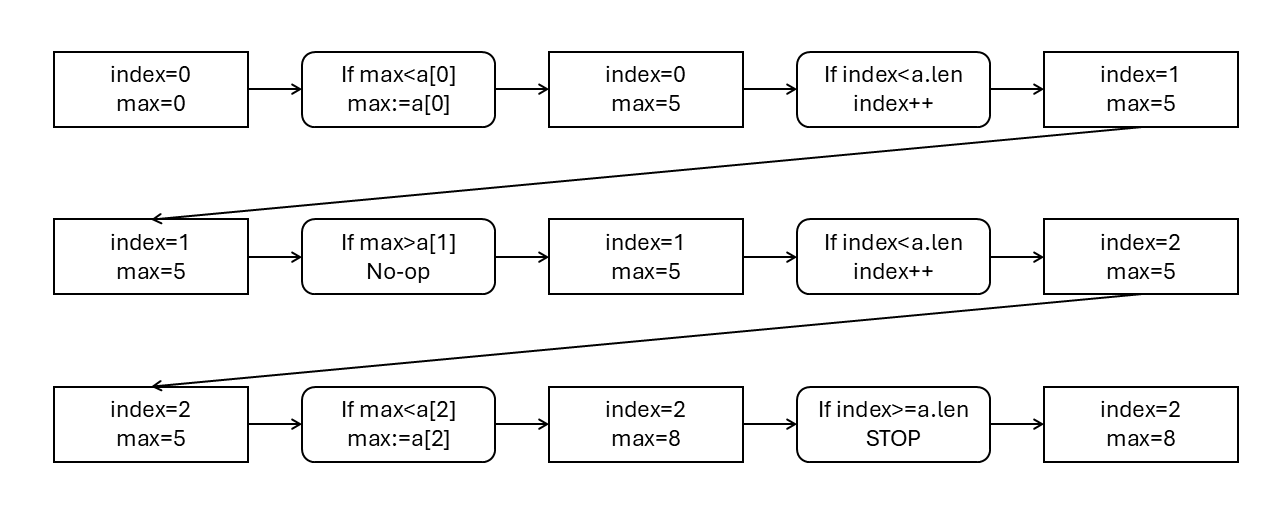
A procedure for a deterministic (classical) computing machine is described as a sequence of steps. After each step, the machine is in a specific state, and the state determines the next step. For example, when iterating through a list of items, the state can be the index of the current item. If the index is less than the length of the list, the next step is to increase the index by one. Otherwise, the next step is to stop the iteration. The following image presents deterministic computation for finding the maximum number in a list. Rectangles represent computation states, and rounded rectangles represent steps. The important point is that there is always exactly one next step.
A procedure for a nondeterministic machine can have multiple next steps after each step. You can think of it as computation splitting and following multiple paths. For example, the following image presents nondeterministic computation for finding a number that divides 15 without remainder.
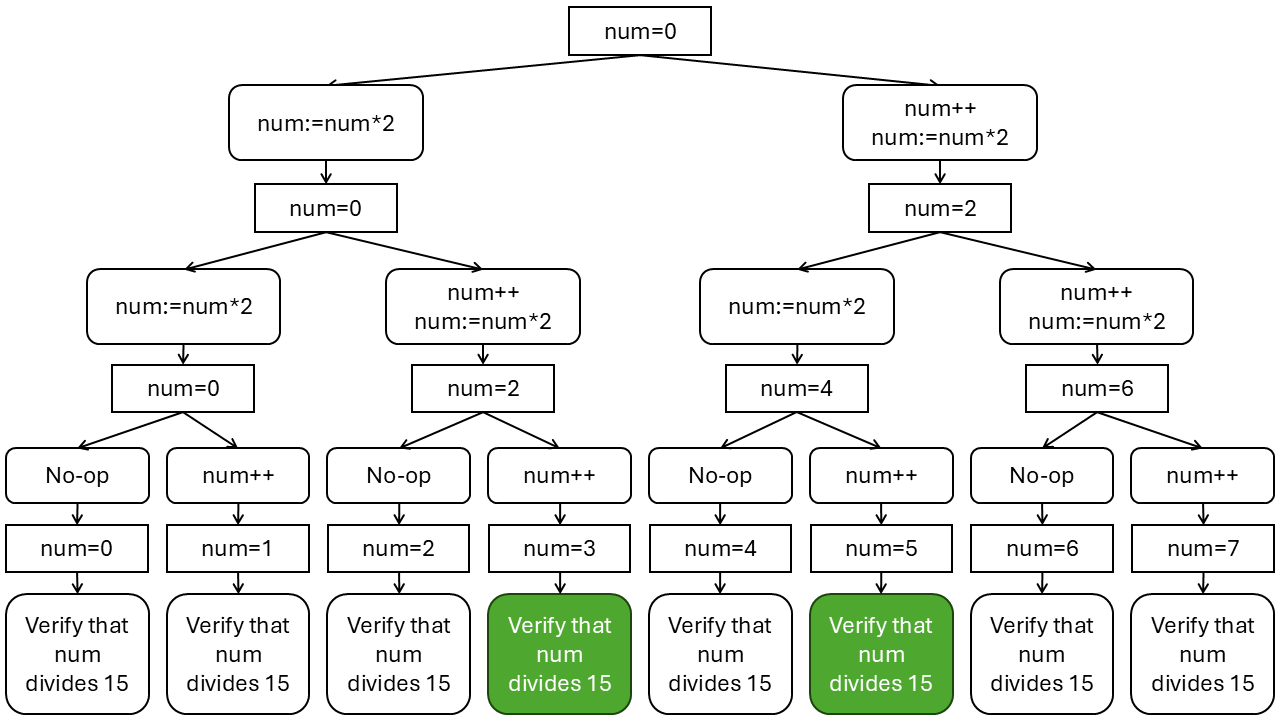
Problems to be solved by nondeterministic machines are usually presented as decision problems, meaning the output is either yes or no. The output is yes if any of the computation paths outputs yes. If all paths output no. then the final output is no. As mentioned, a nondeterministic computing machine is hypothetical, and there can be different actual realizations of such machine. One option is to try all computation paths one by one in sequence. However, for large inputs, there can be a huge number of computation paths. For example, if the input was a 128-bit number, there would be \(2^{128}\) possible computation paths. That is more than the estimated number of atoms in the universe. So that would take too long. Another option is to have multiple processors and try multiple paths in parallel. Parallelism should be easy, because the paths do not have any dependencies. However, it would require an enormous number of processors.
Quantum computer and nondeterminism
Can a quantum computer simulate nondeterministic computing machines efficiently? Yes, for some problems. Recall from the measurement post that multiple qubits can be in superposition of multiple states or numbers with certain probabilities before measurement. Only after the measurement do the qubits collapse to exactly one of the states. It should be possible to map nondeterministic states to quantum states. Then, a quantum computer can compute on the superposition of all nondeterministic states. The following image presents nondeterministic computation of 5 steps with 2 branches at each step, resulting in 32 possible final states. A quantum computer can follow the same computation paths and end in a superposition of 32 final states.
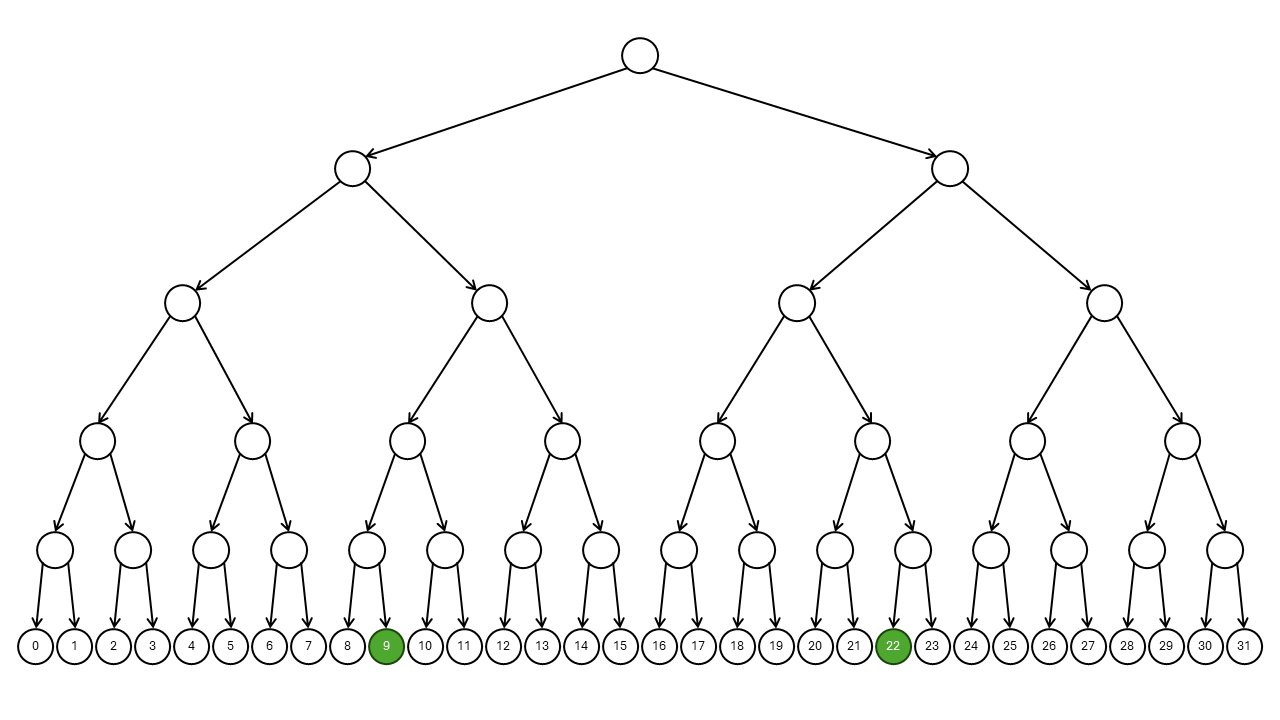
If each of the 32 states has approximately the same probability \(\frac{1}{32}\), then measurement will return any of the states with approximately the same probability. In this case, there are 2 yes states and 30 no states. Therefore, measurement will return yes with probability \(\frac{2}{32}\) and no with probability \(\frac{30}{32}\). So it is much more likely to output no than yes. But no is the wrong answer, because there is at least one yes path.
Can we manipulate the probabilities so that all no states have almost zero probability? If we can do that, then the quantum computer could simulate a nondeterministic computing machine efficiently with high probability.
Quantum Fourier Transform
It seems possible to achieve almost zero probability for no states when each \(k\)-th state is yes state and there are no other yes states. For example, the following image presents nondeterministic computation where every 5th path outputs yes.
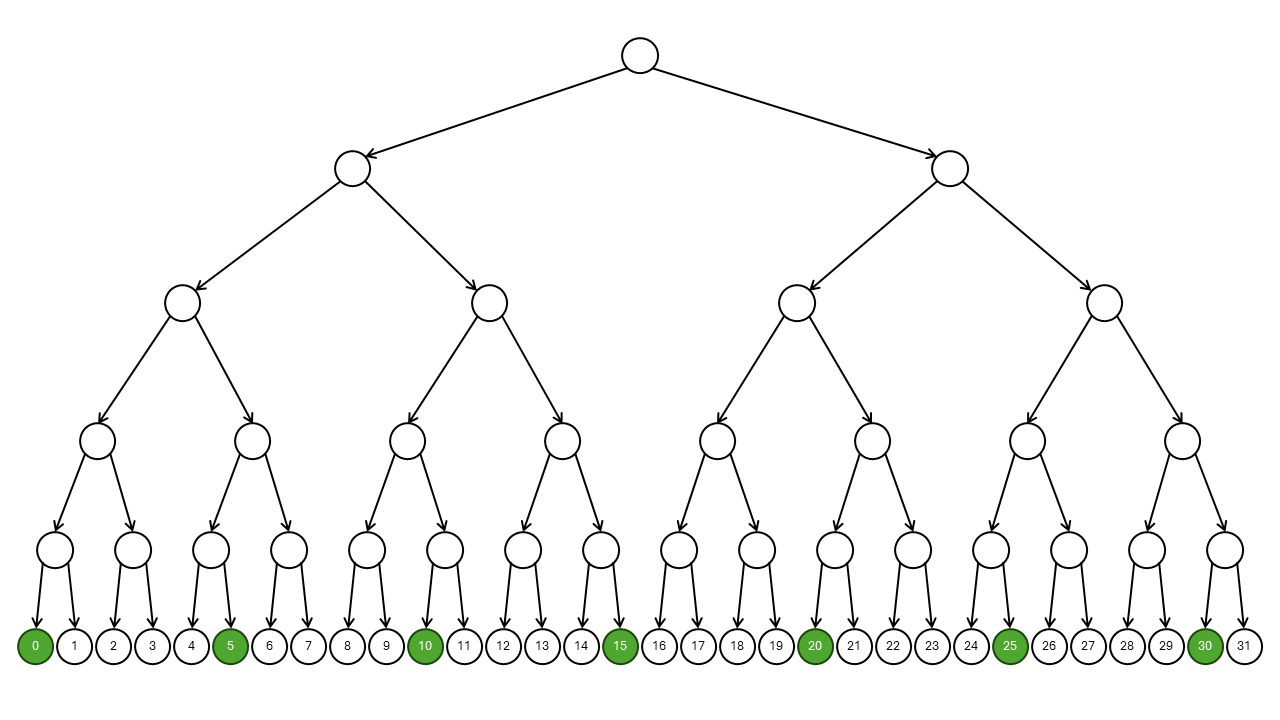
An example of such a problem is Order finding. This is the problem of finding the smallest integer \(r\) such that \(x^r = 1 \mod N\), where \(x\) and \(N\) are given integers. It is easy to verify the solution, but hard to find it. However, the yes states are periodic, occurring at positions \(0, r, 2r, 3r, \ldots\).
If this condition is satisfied, then we can use a method called the Quantum Fourier Transform. I will explain how the method works using a simplified example. You may be familiar with alternating current, which is the electricity available in wall sockets in every household. The voltage of alternating current changes periodically and can be represented as a sine wave.
While there are only 2 wires going to the wall socket, there are 6 wires coming to each household. This is because the electricity provider generates 3 alternating currents, each with the same frequency but shifted by 120° or \(\frac{2\pi}{3}\). This is called 3-phase alternating current. The following image shows 3 sine waves representing the 3 phases of alternating current.
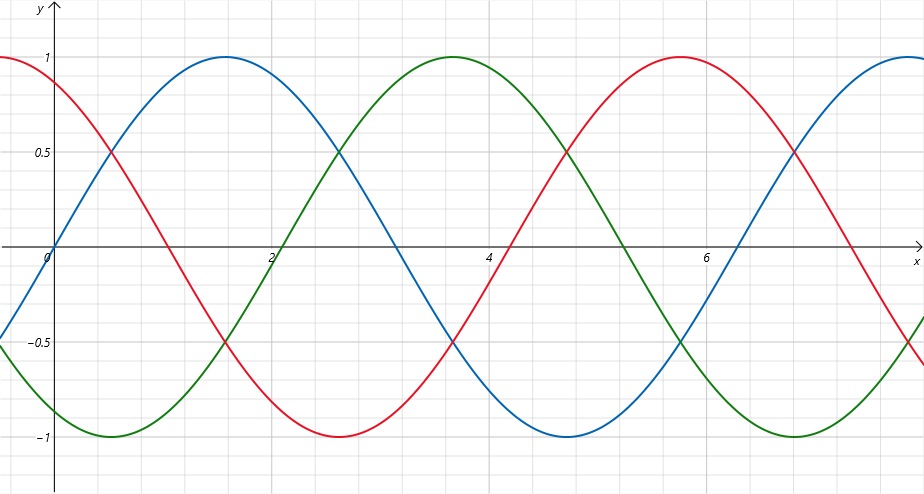
The phase functions are:
Notice that
This means that if we combine the 3 alternating currents, the result is 0. That is why it is possible to use only 4 wires for 3-phase alternating current: 3 wires can be combined into one neutral wire. I may be wrong, I am not an electrician.
Quantum Fourier Transform uses a similar trick. It combines multiple states with different phases in a way that the probability of combined states \(0, 1, \ldots, k-1\) is almost zero. That leaves states \(0, k, 2k, 3k, \ldots\) with high probability. This is exactly what we want to achieve.
An explanation of the Quantum Fourier Transform is beyond the scope of this post. As mentioned, let us consider a problem where every \(k\)-th solution is the correct one. Of course, the value of \(k\) is what we are trying to find. When we find \(k\), we know the solution to our problem. The Quantum Fourier Transform is a procedure to find \(k\).
Summary
A quantum computer can simulate a nondeterministic computing machine efficiently when yes states are periodic. Nondeterministic machines are only a theoretical construct and may be harder to imagine for people outside of computer science. They can be simulated by computers that can run computations in parallel. This is probably the reason why quantum computers are often explained as computers that can run computations in parallel. However, I find the comparison to nondeterministic machines much more insightful. Maybe it is just me, because I have not seen such explanation anywhere else.